Nota Fizik Tingkatan 4 Bab 1: Pengukuran
RINGKASAN
Ringkasan Komprehensif (Nota Fizik Tingkatan 4 Bab 1: Pengukuran)
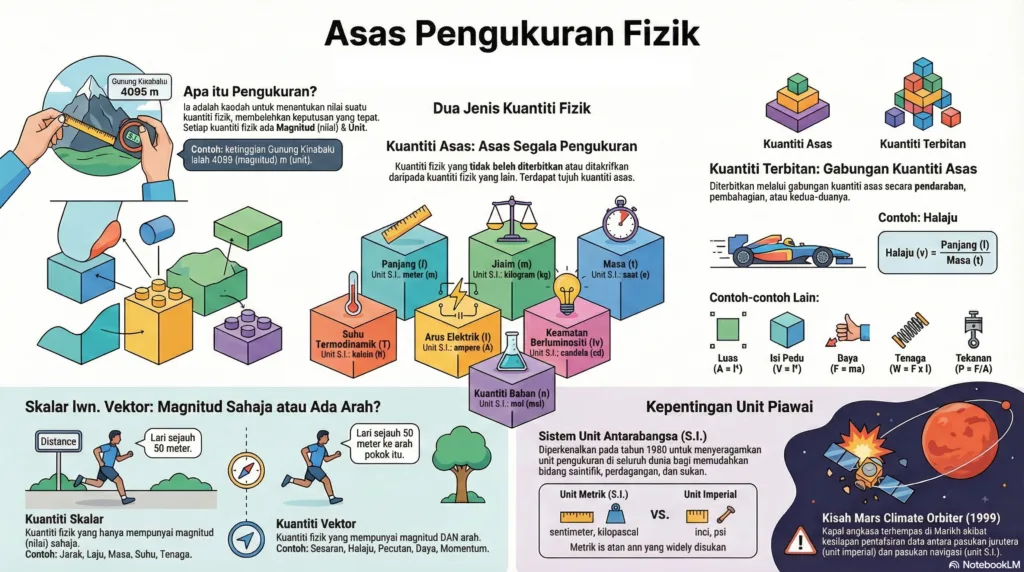
Bab ini memperkenalkan konsep pengukuran sebagai kaedah untuk menentukan nilai suatu kuantiti fizik. Kuantiti fizik, yang sentiasa dinyatakan dengan magnitud dan unit, terbahagi kepada dua kategori utama: kuantiti asas dan kuantiti terbitan.
Kuantiti Asas dan Kuantiti Terbitan:
• Kuantiti Asas adalah kuantiti fizik yang tidak boleh diterbitkan daripada kuantiti fizik yang lain. Terdapat tujuh kuantiti asas yang diiktiraf oleh Sistem Unit Antarabangsa (S.I.):
◦ Panjang (meter, m)
◦ Jisim (kilogram, kg)
◦ Masa (saat, s)
◦ Suhu Termodinamik (kelvin, K)
◦ Arus Elektrik (ampere, A)
◦ Keamatan Berluminositi (candela, cd)
◦ Kuantiti Bahan (mol, mol)
• Kuantiti Terbitan adalah kuantiti fizik yang diperolehi melalui gabungan kuantiti asas secara pendaraban, pembahagian, atau kedua-duanya. Contohnya termasuk luas (m²), isi padu (m³), halaju (m s⁻¹), dan daya (kg m s⁻² atau Newton). Kuantiti terbitan boleh dihuraikan dalam sebutan kuantiti asas dan unit asas S.I. melalui rumus.
Sistem Unit:
• Sistem Unit Antarabangsa (S.I.) telah dipersetujui pada tahun 1960 untuk menyelaraskan sistem pengukuran di seluruh dunia, memudahkan bidang saintifik, perdagangan, dan perubatan.
• Selain unit S.I. (unit metrik), terdapat juga unit imperial seperti inci, kaki, gelen, dan batu. Ketidakseragaman dalam penggunaan unit boleh membawa kepada kesilapan besar, seperti yang berlaku pada kapal angkasa Mars Climate Orbiter pada tahun 1999 yang terhempas akibat kekeliruan antara unit imperial dan unit S.I.
Kuantiti Skalar dan Kuantiti Vektor:
• Kuantiti Skalar ialah kuantiti fizik yang mempunyai magnitud sahaja. Contohnya ialah jarak, laju, masa, suhu, dan tenaga.
• Kuantiti Vektor ialah kuantiti fizik yang mempunyai magnitud dan arah. Contohnya ialah sesaran, halaju, daya, pecutan, dan momentum.
Penyiasatan Saintifik dan Analisis Graf:
• Graf adalah alat penting dalam penyiasatan saintifik untuk memaparkan data dan menentukan hubungan antara dua kuantiti fizik (pemboleh ubah).
• Bentuk graf boleh ditafsirkan untuk memahami hubungan seperti berkadar terus, bertambah secara linear, berkadar songsang, atau hubungan bukan linear yang lain.
• Analisis graf yang lengkap melibatkan lima aspek utama:
1. Menyatakan hubungan antara dua pemboleh ubah.
2. Menentukan kuantiti fizik yang diwakili oleh kecerunan graf.
3. Menentukan nilai kuantiti fizik secara interpolasi (membaca nilai dalam julat data).
4. Membuat ramalan melalui ekstrapolasi (melanjutkan garis graf di luar julat data).
5. Menentukan luas di bawah graf yang mungkin mewakili suatu kuantiti fizik.
• Satu penyiasatan saintifik yang lengkap melibatkan langkah-langkah seperti membuat inferens, hipotesis, mengenal pasti pemboleh ubah (dimanipulasi, bergerak balas, dimalarkan), merancang prosedur, mengumpul dan menganalisis data, serta membuat kesimpulan. Contoh yang diberikan ialah eksperimen bandul ringkas untuk mengkaji hubungan antara panjang bandul (l) dan tempoh ayunan (T).
GLOSARI
| Istilah | Definisi |
| Ekstrapolasi | Proses membuat ramalan nilai di luar julat data yang diplot pada graf dengan memanjangkan garis graf. |
| Graf | Perwakilan visual data yang menunjukkan hubungan antara dua atau lebih pemboleh ubah. |
| Hipotesis | Satu pernyataan awal yang boleh diuji secara saintifik tentang hubungan antara pemboleh ubah dimanipulasi dan pemboleh ubah bergerak balas. |
| Inferens | Kesimpulan awal yang dibuat berdasarkan pemerhatian. |
| Interpolasi | Proses menentukan nilai pada graf yang berada dalam julat data yang telah diplot. |
| Kecerunan | Ukuran kecuraman suatu garis pada graf, dikira sebagai perubahan pada paksi-y dibahagikan dengan perubahan pada paksi-x. |
| Kuantiti Asas | Kuantiti fizik yang tidak boleh diterbitkan daripada kuantiti fizik yang lain. Terdapat tujuh kuantiti asas. |
| Kuantiti Fizik | Kuantiti yang boleh diukur. |
| Kuantiti Skalar | Kuantiti fizik yang hanya mempunyai magnitud. |
| Kuantiti Terbitan | Kuantiti fizik yang diterbitkan daripada gabungan kuantiti-kuantiti asas. |
| Kuantiti Vektor | Kuantiti fizik yang mempunyai magnitud dan arah. |
| Magnitud | Nilai berangka bagi suatu kuantiti fizik. |
| Metrologi | Bidang kajian saintifik mengenai pengukuran dan piawaian. |
| Pemboleh Ubah | Faktor atau keadaan yang boleh berubah dalam suatu penyiasatan saintifik. |
| Pengukuran | Kaedah untuk menentukan nilai suatu kuantiti fizik. |
| Penyiasatan Saintifik | Suatu proses sistematik untuk menyiasat fenomena melalui pemerhatian, eksperimen, dan analisis. |
| Sistem Unit Antarabangsa (S.I.) | Sistem unit pengukuran yang diseragamkan dan digunakan di seluruh dunia untuk tujuan saintifik dan komersial. |
| Tempoh Ayunan (T) | Masa yang diambil untuk melengkapkan satu ayunan yang lengkap. |
| Unit Imperial | Sistem unit pengukuran yang digunakan secara tradisional di beberapa negara, contohnya inci, kaki, gelen, dan batu. |
| Unit Metrik | Sistem unit pengukuran berdasarkan meter, kilogram, dan saat, yang menjadi asas kepada Sistem Unit Antarabangsa (S.I.). |
CONTOH SOALAN KBAT
Soalan Kemahiran Berfikir Aras Tinggi (KBAT)
1. Berdasarkan insiden kapal angkasa Mars Climate Orbiter, jelaskan mengapa penggunaan Sistem Unit Antarabangsa (S.I.) amat kritikal dalam projek-projek antarabangsa pada hari ini seperti Stesen Angkasa Antarabangsa (ISS) dan perdagangan global.
Jawapan: Insiden Mars Climate Orbiter menunjukkan bahawa perbezaan unit yang nampak kecil boleh menyebabkan kegagalan yang besar dan mahal. Dalam projek antarabangsa seperti ISS, komponen-komponen dibina oleh negara yang berbeza (Amerika Syarikat, Rusia, Eropah, Jepun, dll.). Jika setiap negara menggunakan sistem unit sendiri (cth: imperial vs metrik) tanpa penyelarasan yang ketat, komponen tersebut mungkin tidak akan dapat disambung dengan betul, atau sistem perisiannya mungkin akan memberi arahan yang salah. Penggunaan S.I. sebagai piawaian tunggal memastikan semua pihak berkomunikasi menggunakan “bahasa” pengukuran yang sama, mengelakkan salah faham, menjamin keserasian komponen, dan memastikan keselamatan serta kejayaan misi. Dalam perdagangan global, S.I. memudahkan perbandingan harga, kuantiti, dan spesifikasi produk merentasi sempadan, mengurangkan kekeliruan dan pertikaian perdagangan.
2. Dalam eksperimen spring (Aktiviti 1.3), graf F melawan x menghasilkan garis lurus yang melalui asalan. Apakah kesimpulan yang boleh dibuat tentang hubungan antara daya, F, dengan pemanjangan spring, x? Jika spring yang lebih keras digunakan, bagaimanakah rupa graf yang baharu berbanding graf asal? Jelaskan.
Jawapan: Kesimpulan yang boleh dibuat ialah daya, F, adalah berkadar terus dengan pemanjangan spring, x. Ini kerana graf garis lurus yang melalui asalan menunjukkan hubungan perkadaran terus. Jika spring yang lebih keras digunakan, ia memerlukan daya yang lebih besar untuk menghasilkan pemanjangan yang sama. Oleh itu, kecerunan graf, k (pemalar daya), akan menjadi lebih besar. Graf yang baharu masih akan berbentuk garis lurus yang melalui asalan, tetapi ia akan lebih curam berbanding graf asal.
3. Rujuk petikan tentang Puan Aishah yang memandu ke Kota Kinabalu. Kenal pasti SEMUA kuantiti asas, kuantiti terbitan, kuantiti skalar, dan kuantiti vektor daripada petikan tersebut dan kelaskan dalam satu jadual.
Jawapan:
| Kategori | Kuantiti Fizik | Nilai |
| Kuantiti Skalar | Jarak | 333 km |
| Laju | 80 km j⁻¹ | |
| Masa | 3 jam | |
| Kuantiti Vektor | Pecutan | 1.2 m s⁻² |
| Kuantiti Asas | Masa | 3 jam |
| Panjang (digunakan untuk terbitkan jarak) | 333 km | |
| Kuantiti Terbitan | Jarak | 333 km |
| Laju | 80 km j⁻¹ | |
| Pecutan | 1.2 m s⁻² |
Nota: Jarak ialah kuantiti skalar tetapi terbitan daripada kuantiti asas panjang. Laju ialah kuantiti skalar terbitan. Pecutan ialah kuantiti vektor terbitan.
4. Dalam eksperimen bandul ringkas, prosedur menyatakan bahawa sudut ayunan mestilah kurang daripada 10°. Ramalkan apakah yang akan berlaku pada nilai tempoh ayunan, T, jika eksperimen diulang dengan sudut ayunan yang besar (cth: 45°). Justifikasikan ramalan anda.
Jawapan: Jika eksperimen diulang dengan sudut ayunan yang besar, nilai tempoh ayunan, T, yang diukur akan menjadi lebih panjang daripada nilai yang dijangkakan oleh rumus T² ∝ l. Rumus yang digunakan dalam buku teks adalah penghampiran yang hanya tepat untuk sudut ayunan yang kecil (< 10°). Apabila sudut ayunan menjadi besar, tempoh ayunan tidak lagi bergantung semata-mata pada panjang tali, tetapi juga mula dipengaruhi oleh amplitud (sudut) ayunan itu sendiri. Oleh itu, untuk memastikan hanya hubungan antara panjang dan tempoh dikaji (menjadikan pemboleh ubah lain dimalarkan), sudut ayangan perlu dikekalkan kecil.
5. Hukum Kegravitian Semesta Newton dinyatakan sebagai F = GMm/r². Berdasarkan persamaan ini, terbitkan unit bagi pemalar kegravitian, G, dalam sebutan unit asas S.I. dan jelaskan mengapa daya, F, ialah suatu kuantiti vektor.
Jawapan: Untuk menerbitkan unit G, susun semula persamaan: G = Fr² / Mm. Gantikan unit S.I. bagi setiap kuantiti:
• Unit F (Daya) = N = kg m s⁻²
• Unit r (Jarak) = m
• Unit M dan m (Jisim) = kg Unit G = (kg m s⁻²) (m²) / (kg × kg) Unit G = (kg m³ s⁻²) / (kg²) Unit G = kg⁻¹ m³ s⁻²
Daya, F, ialah suatu kuantiti vektor kerana ia mempunyai magnitud (kekuatan daya tarikan) dan arah. Dalam konteks ini, arah daya graviti sentiasa bertindak di sepanjang garis yang menyambungkan pusat jisim kedua-dua jasad (M dan m). Ia adalah daya tarikan, jadi arahnya adalah ke arah jasad yang lain.
