Nota Fizik Tingkatan 4 Bab 3: Kegravitian
RINGKASAN
Ringkasan (Nota Fizik Tingkatan 4 Bab 3: Kegravitian)
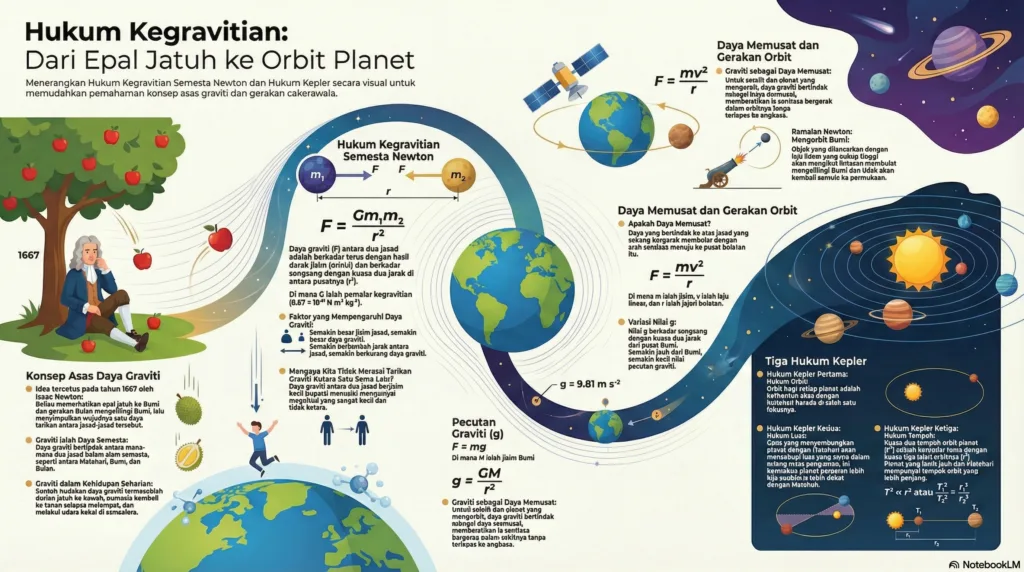
Bab ini meneroka konsep-konsep asas kegravitian, bermula dengan Hukum Kegravitian Semesta Newton dan diakhiri dengan Hukum Kepler mengenai gerakan planet.
Hukum Kegravitian Semesta Newton
Dikemukakan oleh Isaac Newton pada tahun 1687, hukum ini menyatakan bahawa daya tarikan graviti wujud di antara mana-mana dua jasad dalam alam semesta. Daya ini adalah daya semesta yang bertindak antara objek seperti epal dan Bumi, Bulan dan Bumi, serta Matahari dan planet-planet.
Hubungan utama hukum ini adalah:
1. Daya graviti (F) berkadar terus dengan hasil darab jisim kedua-dua jasad (m₁m₂). Ini bermakna semakin besar jisim jasad, semakin besar daya graviti.
2. Daya graviti (F) berkadar songsang dengan kuasa dua jarak (r²) di antara pusat kedua-dua jasad. Ini bermakna semakin jauh jarak antara jasad, semakin lemah daya graviti.
Hubungan ini dirumuskan dalam formula: F = Gm₁m₂ / r² di mana:
• F ialah daya graviti.
• m₁ dan m₂ ialah jisim kedua-dua jasad.
• r ialah jarak antara pusat kedua-dua jasad.
• G ialah pemalar kegravitian semesta, dengan nilai 6.67 × 10⁻¹¹ N m² kg⁻².
Daya graviti wujud secara berpasangan dengan magnitud yang sama, tetapi kesannya lebih ketara pada jasad yang mempunyai jisim yang lebih kecil.
Pecutan Graviti (g) dan Pemalar Kegravitian (G)
Pecutan graviti, g, di permukaan Bumi boleh dihubungkaitkan dengan pemalar kegravitian semesta, G. Dengan menyamakan Hukum Gerakan Newton Kedua (F = mg) dan Hukum Kegravitian Semesta Newton (F = GMm/r²), kita memperoleh rumus untuk pecutan graviti: g = GM / r² di mana:
• M ialah jisim Bumi.
• r ialah jarak dari pusat Bumi.
Di permukaan Bumi, r adalah sama dengan jejari Bumi (R), jadi g = GM / R². Nilai g berubah dengan ketinggian; ia berkadar songsang dengan kuasa dua jarak dari pusat Bumi. Pengetahuan tentang pecutan graviti adalah penting untuk penerokaan angkasa dan memahami kelangsungan hidup.
Daya Memusat dalam Gerakan Satelit dan Planet
Jasad yang melakukan gerakan membulat seragam, seperti satelit yang mengorbit Bumi, sentiasa mengalami perubahan arah gerakan. Ini memerlukan satu daya yang bertindak ke arah pusat bulatan, yang dikenali sebagai daya memusat. Formula daya memusat ialah: F = mv² / r di mana:
• m ialah jisim jasad.
• v ialah laju linear.
• r ialah jejari bulatan (orbit).
Bagi satelit dan planet, daya graviti bertindak sebagai daya memusat yang mengekalkan mereka dalam orbit.
Hukum Kepler
Johannes Kepler merumuskan tiga hukum yang menghuraikan gerakan planet mengelilingi Matahari:
1. Hukum Kepler Pertama: Orbit bagi setiap planet adalah elips dengan Matahari berada di salah satu daripada fokusnya.
2. Hukum Kepler Kedua: Garis yang menyambungkan planet dengan Matahari akan mencakupi luas yang sama dalam selang masa yang sama. Ini bermakna planet bergerak lebih laju apabila ia lebih dekat dengan Matahari dan lebih perlahan apabila ia lebih jauh.
3. Hukum Kepler Ketiga: Kuasa dua tempoh orbit planet (T²) adalah berkadar terus dengan kuasa tiga jejari orbitnya (r³). Ini dinyatakan sebagai T² ∝ r³. Planet yang lebih jauh dari Matahari mempunyai tempoh orbit yang lebih panjang.
Hukum ini boleh dirumuskan sebagai: T₁²/T₂² = r₁³/r₂³
GLOSARI
| Istilah | Definisi |
| Daya Graviti | Daya tarikan semesta yang bertindak antara mana-mana dua jasad yang mempunyai jisim dalam alam semesta. |
| Daya Memusat | Suatu daya yang bertindak ke atas jasad yang melakukan gerakan membulat dengan arah yang sentiasa menuju ke pusat bulatan itu. |
| Daya Semesta | Sifat daya graviti yang bertindak antara mana-mana dua jasad dalam alam semesta, tanpa mengira saiz atau jarak. |
| Elips | Bentuk geometri bujur yang merupakan bentuk orbit planet mengikut Hukum Kepler Pertama. Ia mempunyai dua titik fokus. |
| Gerakan Membulat Seragam | Pergerakan suatu jasad dalam bulatan dengan laju yang seragam, walaupun arah gerakannya sentiasa berubah. |
| Hukum Kegravitian Semesta Newton | Menyatakan bahawa daya graviti antara dua jasad adalah berkadar terus dengan hasil darab jisim kedua-dua jasad dan berkadar songsang dengan kuasa dua jarak di antara pusat dua jasad tersebut. |
| Hukum Kepler Pertama | Menyatakan bahawa orbit bagi setiap planet adalah elips dengan Matahari berada di salah satu daripada fokusnya. |
| Hukum Kepler Kedua | Menyatakan bahawa garis yang menyambungkan planet dengan Matahari akan mencakupi luas yang sama dalam selang masa yang sama. |
| Hukum Kepler Ketiga | Menyatakan bahawa kuasa dua tempoh orbit planet (T²) adalah berkadar terus dengan kuasa tiga jejari orbitnya (r³). |
| Laju Linear (v) | Laju jasad pada suatu ketika tertentu semasa jasad membuat gerakan membulat. |
| Paksi Major | Garis pusat terpanjang bagi sebuah elips, yang melalui kedua-dua titik fokus. |
| Paksi Minor | Garis pusat terpendek bagi sebuah elips, yang berserenjang dengan paksi major. |
| Pecutan Graviti (g) | Pecutan yang dialami oleh objek yang jatuh bebas disebabkan oleh daya graviti. Di permukaan Bumi, nilainya kira-kira 9.81 m s⁻². |
| Pemalar Kegravitian (G) | Satu pemalar semesta dalam formula Hukum Kegravitian Semesta Newton, dengan nilai 6.67 × 10⁻¹¹ N m² kg⁻². |
| Tempoh Orbit (T) | Masa yang diambil oleh sebuah planet atau satelit untuk melengkapkan satu orbit penuh. |
CONTOH SOALAN KBAT
Soalan Kemahiran Berfikir Aras Tinggi (KBAT)
1. Seorang angkasawan di Stesen Angkasa Antarabangsa (ISS) kelihatan terapung seolah-olah tiada graviti. Walau bagaimanapun, ISS mengorbit pada ketinggian di mana pecutan graviti Bumi masih kira-kira 90% daripada nilai di permukaan. Jelaskan mengapa angkasawan mengalami keadaan ‘ketiadaan berat’ (weightlessness).
Jawapan: Keadaan ‘ketiadaan berat’ berlaku kerana angkasawan dan stesen angkasa berada dalam keadaan jatuh bebas yang berterusan mengelilingi Bumi. Daya graviti Bumi masih bertindak ke atas mereka, tetapi daya ini berfungsi sebagai daya memusat yang diperlukan untuk mengekalkan mereka dalam orbit. Oleh kerana kedua-dua angkasawan dan stesen angkasa jatuh ke arah Bumi pada kadar pecutan yang sama, angkasawan itu kelihatan terapung relatif kepada stesen tersebut.
2. Andaikan sebuah planet baharu ditemui dengan jisim yang sama seperti Bumi tetapi jejarinya dua kali ganda lebih besar. Apakah nilai pecutan graviti, g, di permukaan planet baharu ini berbanding dengan g di Bumi?
Jawapan: Rumus pecutan graviti ialah g = GM/R². Jika jisim (M) adalah malar dan jejari (R) menjadi dua kali ganda (2R), maka nilai g baharu akan menjadi g’ = GM/(2R)² = GM/(4R²) = (1/4) * (GM/R²). Oleh itu, pecutan graviti di permukaan planet baharu itu adalah satu perempat (1/4) daripada nilai pecutan graviti di Bumi.
3. Sebuah komet mempunyai orbit yang sangat elips mengelilingi Matahari. Menggunakan Hukum Kepler Kedua, huraikan bagaimana kelajuan komet berubah sepanjang perjalanannya dalam orbit. J
awapan: Menurut Hukum Kepler Kedua, garis yang menyambungkan komet dengan Matahari akan mencakupi luas yang sama dalam selang masa yang sama. Untuk berbuat demikian, komet mesti bergerak dengan laju linear yang sangat tinggi apabila ia berada paling dekat dengan Matahari (perihelion) dan bergerak dengan sangat perlahan apabila ia berada paling jauh dari Matahari (aphelion). Laju komet berubah secara berterusan sepanjang orbitnya.
4. Dua satelit, A dan B, mengorbit Bumi. Jejari orbit satelit A adalah empat kali ganda jejari orbit satelit B. Bandingkan tempoh orbit kedua-dua satelit tersebut. Jawapan: Menurut Hukum Kepler Ketiga, T² ∝ r³. Kita boleh menggunakan nisbah Tₐ²/Tₑ² = rₐ³/rₑ³. Diberi rₐ = 4rₑ. Maka, Tₐ² = Tₑ² × (4rₑ)³ / rₑ³ = Tₑ² × (64rₑ³/rₑ³) = 64Tₑ². Dengan mengambil punca kuasa dua, Tₐ = √64 × Tₑ = 8Tₑ. Jadi, tempoh orbit satelit A adalah lapan kali lebih panjang daripada tempoh orbit satelit B.
5. Isaac Newton meramalkan bahawa jika sebiji peluru meriam dilancarkan dari puncak gunung yang sangat tinggi dengan laju linear yang mencukupi, ia tidak akan jatuh semula ke Bumi tetapi akan terus mengorbit Bumi. Terangkan konsep ini menggunakan prinsip daya graviti dan daya memusat.
Jawapan: Apabila peluru dilancarkan secara mengufuk, ia akan jatuh ke Bumi disebabkan oleh daya graviti. Namun, jika laju linearnya cukup tinggi, semasa ia jatuh, permukaan Bumi yang melengkung juga akan ‘jatuh’ daripadanya. Pada laju tertentu, lengkungan trajektori peluru akan sepadan dengan lengkungan permukaan Bumi. Pada ketika ini, daya graviti yang sentiasa menarik peluru ke arah pusat Bumi tidak lagi menyebabkannya menghampiri permukaan, sebaliknya ia berfungsi sebagai daya memusat yang diperlukan untuk mengekalkan peluru dalam orbit yang stabil mengelilingi Bumi.
