Nota Fizik Tingkatan 5 Bab 1: Daya Dan Gerakan II
Koleksi Latihan
| 1 | 2 |
| 3 | 4 |
| 5 | 6 |
RINGKASAN
Ringkasan Mudah Difahami (Nota Fizik Tingkatan 5 Bab 1: Daya Dan Gerakan II)
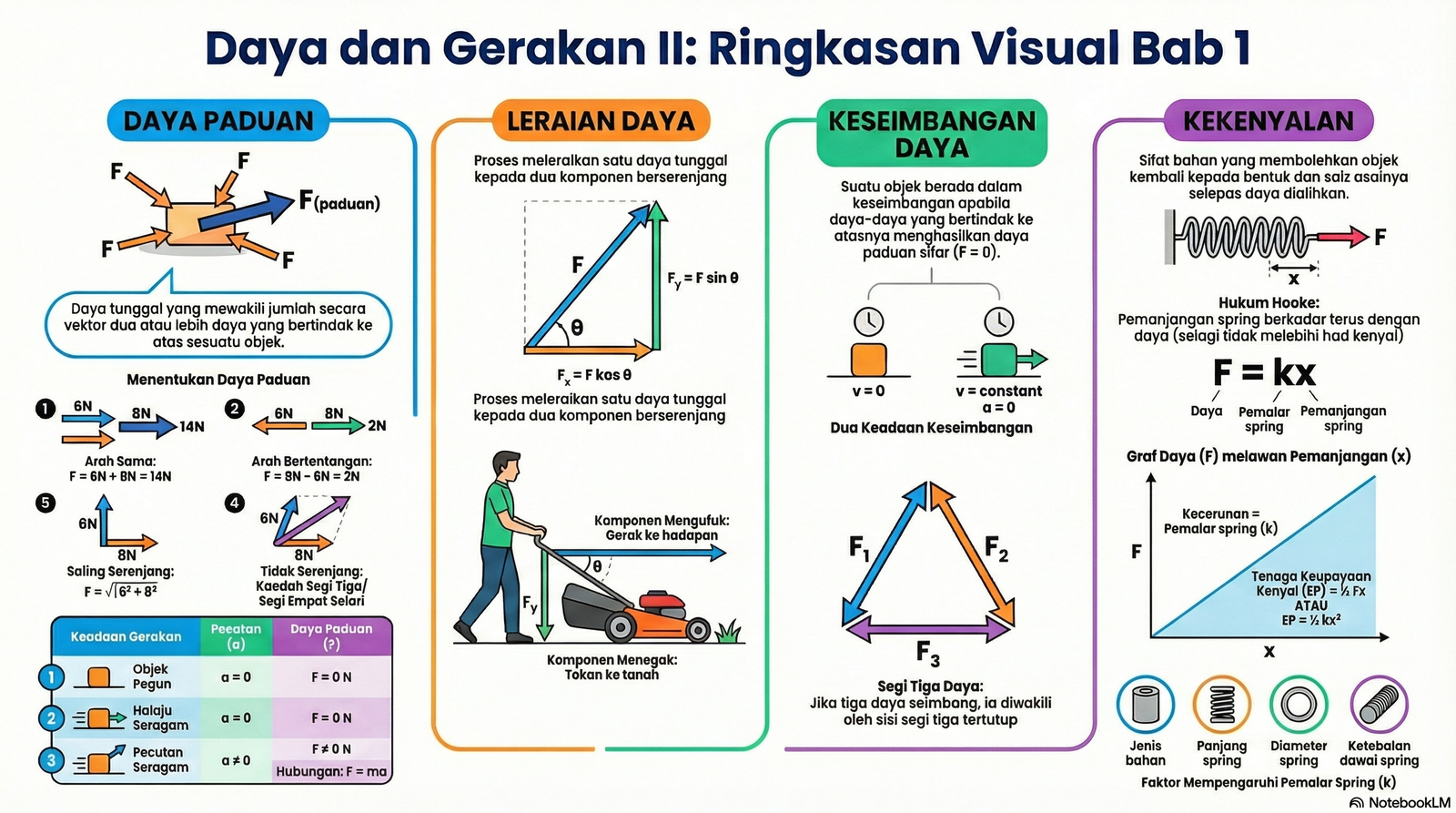
Bab ini meneroka interaksi daya dan kesannya terhadap keadaan pegun dan gerakan objek. Konsep-konsep ini adalah asas dalam bidang kejuruteraan, seni bina, dan fizik.
1. Daya Paduan
Daya paduan ialah daya tunggal yang mewakili kesan gabungan (jumlah secara vektor) dua atau lebih daya yang bertindak ke atas sesuatu objek. Keadaan gerakan objek ditentukan oleh daya paduan ini:
• Daya Paduan Sifar (F = 0): Objek sama ada kekal dalam keadaan pegun atau bergerak dengan halaju seragam. Ini berlaku apabila daya-daya yang bertindak adalah seimbang. Contohnya, jika dua daya yang sama magnitud bertindak pada arah bertentangan.
• Daya Paduan Bukan Sifar (F ≠ 0): Objek akan mengalami pecutan (perubahan halaju) mengikut arah daya paduan tersebut. Hubungan ini diterangkan oleh Hukum Gerakan Newton Kedua, F = ma, di mana F ialah daya paduan, m ialah jisim, dan a ialah pecutan.
Penentuan daya paduan bergantung pada arah daya-daya yang bertindak:
• Arah Sama: Magnitud dijumlahkan.
• Arah Bertentangan: Magnitud yang lebih kecil ditolak daripada yang lebih besar.
• Saling Berserenjang: Magnitud ditentukan menggunakan Teorem Pythagoras.
• Tidak Berserenjang: Magnitud dan arah ditentukan menggunakan kaedah segi tiga daya atau kaedah segi empat selari daya.
2. Leraian Daya
Leraian daya adalah proses menguraikan satu daya tunggal kepada dua komponen yang saling berserenjang (biasanya komponen mengufuk, Fx, dan komponen menegak, Fy). Ini amat berguna untuk menganalisis daya yang bertindak pada suatu sudut.
• Komponen Mengufuk: Fx = F kos θ
• Komponen Menegak: Fy = F sin θ
Proses ini membolehkan analisis yang lebih mudah, seperti mengira bagaimana daya tarikan pada suatu sudut boleh menggerakkan objek secara mengufuk sambil mengurangkan sebahagian beratnya secara menegak.
3. Keseimbangan Daya
Suatu objek dikatakan berada dalam keseimbangan daya apabila daya-daya yang bertindak ke atasnya menghasilkan daya paduan sifar (F = 0). Ini bermakna objek itu sama ada pegun atau bergerak dengan halaju seragam. Apabila tiga daya berada dalam keseimbangan, ia boleh diwakili oleh sebuah segi tiga daya yang tertutup, di mana setiap sisi mewakili magnitud dan arah salah satu daya.
4. Kekenyalan
Kekenyalan ialah sifat bahan yang membolehkannya kembali kepada bentuk dan saiz asal selepas daya luar yang mengubahnya dialihkan.
• Hukum Hooke: Menyatakan bahawa pemanjangan spring (x) adalah berkadar terus dengan daya (F) yang dikenakan ke atasnya, selagi tidak melebihi had kenyal. Rumusnya ialah F = kx.
• Pemalar Spring (k): Ukuran kekerasan atau ketegaran spring. Ia mewakili daya yang diperlukan untuk menghasilkan seunit pemanjangan. Nilai k boleh ditentukan daripada kecerunan graf daya melawan pemanjangan.
• Faktor Mempengaruhi Pemalar Spring: Nilai k dipengaruhi oleh bahan spring, panjang spring, diameter spring, dan ketebalan dawai spring.
• Tenaga Keupayaan Kenyal (EP): Tenaga yang disimpan dalam spring apabila ia diregangkan atau dimampatkan. Ia dikira sebagai luas di bawah graf F melawan x, dengan rumus EP = ½ Fx atau EP = ½ kx².
GLOSARI
| Istilah | Definisi |
| Daya Paduan | Daya tunggal yang mewakili jumlah secara vektor dua atau lebih daya yang bertindak ke atas sesuatu objek. |
| Gambar Rajah Jasad Bebas | Gambar rajah yang menunjukkan semua daya yang bertindak ke atas objek itu sahaja. |
| Had Kenyal | Had maksimum daya yang boleh dikenakan ke atas suatu bahan anjal sebelum ia tidak dapat kembali kepada bentuk dan saiz asalnya. |
| Hukum Hooke | Menyatakan bahawa pemanjangan suatu spring adalah berkadar terus dengan daya yang bertindak ke atas spring jika tidak melebihi had kenyal spring itu. Rumusnya ialah F = kx. |
| Kekenyalan | Sifat bahan yang membolehkan suatu objek kembali kepada bentuk dan saiz asalnya selepas daya yang bertindak ke atasnya dialihkan. |
| Keseimbangan Daya | Keadaan apabila daya-daya yang bertindak ke atas suatu objek menghasilkan daya paduan sifar, menyebabkan objek itu pegun atau bergerak dengan halaju seragam. |
| Leraian Daya | Proses meleraikan satu daya tunggal kepada komponen-komponen daya (biasanya dua komponen yang saling berserenjang). |
| Pemalar Spring (k) | Suatu pemalar yang mewakili kekerasan spring. Ia adalah nisbah daya kepada pemanjangan spring (k = F/x). |
| Pemanjangan Spring (x) | Penambahan panjang spring apabila daya regangan dikenakan ke atasnya, dihitung dengan x = l – l₀, di mana l ialah panjang diregangkan dan l₀ ialah panjang asal. |
| Segi Tiga Daya | Sebuah gambar rajah vektor di mana tiga daya dalam keseimbangan diwakili oleh tiga sisi sebuah segi tiga yang dilukis secara berturutan. |
| Tenaga Keupayaan Kenyal (EP) | Tenaga yang disimpan dalam suatu objek anjal (seperti spring) apabila ia diregangkan atau dimampatkan. Dihitung menggunakan EP = ½ Fx atau EP = ½ kx². |
CONTOH SOALAN KBAT
Soalan Kemahiran Berfikir Aras Tinggi (KBAT)
Berikut adalah lima soalan yang memerlukan analisis dan aplikasi mendalam terhadap prinsip-prinsip fizik yang telah dipelajari.
Soalan 1: Merujuk kepada penerangan mengenai Langkawi Skybridge, jelaskan bagaimana konsep keseimbangan daya, leraian daya, dan daya paduan diaplikasikan oleh jurutera untuk memastikan jambatan gantung sepanjang 125 meter itu kekal stabil walaupun hanya disokong oleh satu pilon condong dan terdedah kepada daya luar seperti angin dan pergerakan pelancong.
Jawapan: Para jurutera mengaplikasikan prinsip-prinsip fizik secara bersepadu untuk memastikan kestabilan Langkawi Skybridge:
1. Analisis Daya Luar: Jurutera mengenal pasti semua daya yang bertindak ke atas jambatan, termasuk berat jambatan itu sendiri (W), beban daripada pelancong, dan daya tiupan angin. Semua daya ini adalah kuantiti vektor yang mempunyai magnitud dan arah.
2. Leraian Daya: Setiap daya ini, terutamanya daya daripada lapan utas kabel yang menegang pada sudut tertentu, dileraikan kepada komponen mengufuk (Fx) dan komponen menegak (Fy). Ini membolehkan jurutera menganalisis kesan daya pada setiap paksi secara berasingan.
3. Keseimbangan Daya: Untuk jambatan berada dalam keadaan stabil (pegun atau dalam keseimbangan), daya paduan yang bertindak ke atasnya mestilah sifar (F=0). Ini bermakna:
◦ Jumlah semua komponen daya menegak yang bertindak ke atas adalah sama dengan jumlah semua komponen daya menegak yang bertindak ke bawah. Daya tegangan menegak daripada kabel dan daya tujah ke atas daripada pilon mengimbangi berat keseluruhan jambatan dan beban pelancong.
◦ Jumlah semua komponen daya mengufuk ke kanan adalah sama dengan jumlah semua komponen daya mengufuk ke kiri. Reka bentuk pilon dan sistem kabel direka untuk menghasilkan daya yang mengimbangi daya angin dan sebarang daya sisi yang lain. Dengan memastikan daya paduan dalam kedua-dua arah mengufuk dan menegak adalah sifar, jambatan tersebut mencapai keseimbangan daya dan kekal teguh serta selamat untuk digunakan.
Soalan 2: Sebuah kenderaan memerlukan sistem ampaian (suspension) untuk menyerap hentakan dari jalan yang tidak rata. Dengan menggunakan pengetahuan anda tentang susunan spring secara sesiri dan selari serta faktor-faktor yang mempengaruhi pemalar spring, cadangkan reka bentuk sistem spring yang paling berkesan untuk tujuan ini. Justifikasikan cadangan anda.
Jawapan: Cadangan reka bentuk yang paling berkesan adalah menggunakan beberapa spring yang disusun secara selari dan diperbuat daripada bahan dengan pemalar spring (k) yang tinggi. Justifikasi:
1. Susunan Selari: Apabila spring disusun secara selari, daya (beban kenderaan) diagihkan antara spring-spring tersebut. Ini menjadikan sistem secara keseluruhan lebih keras dan lebih sukar untuk dimampatkan berbanding susunan sesiri. Pemalar spring berkesan bagi sistem selari adalah lebih tinggi. Ini penting untuk menampung berat kenderaan yang besar tanpa termampat sepenuhnya, sambil masih membenarkan pergerakan untuk menyerap hentakan.
2. Pemalar Spring Tinggi: Menurut Jadual 1.7, pemalar spring yang tinggi boleh dicapai dengan menggunakan dawai yang lebih tebal, diameter spring yang lebih kecil, atau bahan yang lebih keras. Spring yang keras (k tinggi) mampu menyimpan lebih banyak tenaga keupayaan kenyal untuk pemampatan yang sama, membolehkannya menolak kembali dengan daya yang kuat untuk mengembalikan kenderaan ke kedudukan asalnya selepas hentakan. Gabungan susunan selari dan spring dengan pemalar spring yang tinggi menghasilkan sistem ampaian yang teguh, stabil, dan cekap menyerap hentakan, sesuai untuk kenderaan.
Soalan 3: Seorang penumpang berjisim 60 kg berada di dalam sebuah lif. Terangkan bagaimana magnitud tindak balas normal (R) daripada lantai lif berubah dan apakah yang dirasai oleh penumpang itu dalam tiga keadaan: (i) lif memecut ke atas, (ii) lif bergerak ke atas dengan halaju seragam, dan (iii) lif dalam keadaan pegun.
Jawapan: Perasaan “berat” seseorang ditentukan oleh magnitud daya tindak balas normal (R) yang bertindak ke atasnya. Berat sebenar penumpang (W = mg) adalah malar.
1. (i) Lif Memecut ke Atas (a > 0): Terdapat daya paduan (F) ke atas (F = ma). Ini bermakna daya ke atas (R) mesti lebih besar daripada daya ke bawah (W).
◦ F = R – W = ma ⇒ R = W + ma.
◦ Oleh kerana R > W, penumpang akan berasa lebih berat daripada biasa.
2. (ii) Lif Bergerak dengan Halaju Seragam (a = 0): Apabila halaju seragam, pecutan adalah sifar. Maka, daya paduan (F) juga sifar.
◦ F = R – W = 0 ⇒ R = W.
◦ Magnitud tindak balas normal adalah sama dengan berat penumpang. Penumpang akan berasa berat seperti biasa.
3. (iii) Lif dalam Keadaan Pegun (a = 0): Sama seperti bergerak dengan halaju seragam, pecutan adalah sifar dan daya paduan adalah sifar.
◦ F = R – W = 0 ⇒ R = W.
◦ Penumpang juga akan berasa berat seperti biasa.
Soalan 4: Dalam menyelesaikan masalah yang melibatkan tiga daya dalam keseimbangan, seperti kotak pegun di atas satah condong, dua kaedah boleh digunakan: melukis segi tiga daya berskala atau menggunakan leraian daya untuk pengiraan. Bandingkan kedua-dua kaedah ini dari segi kejituan, kemudahan penggunaan, dan maklumat yang diperoleh.
Jawapan: Perbandingan antara kaedah segi tiga daya berskala dan kaedah leraian daya:
• Kejituan: Kaedah leraian daya (pengiraan) adalah lebih jitu. Jawapannya adalah tepat secara matematik. Kaedah segi tiga daya berskala bergantung kepada ketepatan lukisan dan pengukuran menggunakan pembaris dan jangka sudut, yang terdedah kepada ralat paralaks dan kepekaan alat. Seperti yang dinyatakan dalam nota teks, “Kaedah penghitungan memberi jawapan yang lebih jitu”.
• Kemudahan Penggunaan: Bagi sesetengah orang, melukis gambar rajah berskala mungkin lebih mudah dan intuitif untuk memvisualisasikan hubungan antara daya-daya. Walau bagaimanapun, ia memerlukan alatan melukis. Kaedah leraian daya memerlukan pemahaman trigonometri (sin, kos, tan) tetapi boleh diselesaikan dengan cepat menggunakan kalkulator tanpa perlu melukis.
• Maklumat yang Diperoleh: Kedua-dua kaedah boleh digunakan untuk mencari magnitud dan arah daya yang tidak diketahui. Kaedah leraian daya secara semula jadi memisahkan masalah kepada komponen-komponen berserenjang, yang selalunya berguna untuk analisis lanjut (contohnya, mengira daya geseran atau pecutan). Gambar rajah berskala memberikan gambaran keseluruhan hubungan vektor secara visual.
Soalan 5: Rajah 1.2 menunjukkan tiga situasi dalam pertandingan tarik tali. Jika kedua-dua pasukan mempunyai kekuatan yang hampir sama, pertandingan itu mungkin berlanjutan lama. Cadangkan dua pengubahsuaian, berdasarkan prinsip fizik, yang boleh dilakukan oleh satu pasukan untuk meningkatkan peluang mereka untuk menang (iaitu, menghasilkan daya paduan yang lebih besar ke arah mereka).
Jawapan: Untuk menang, sesebuah pasukan perlu menghasilkan daya tarikan yang lebih besar daripada pasukan lawan supaya wujud daya paduan bersih ke arah mereka. Dua pengubahsuaian berdasarkan prinsip fizik ialah:
1. Meningkatkan Daya Geseran: Kemenangan dalam tarik tali bukan sahaja bergantung pada kekuatan menarik tali, tetapi juga pada keupayaan untuk “mencengkam” tanah. Daya geseran antara kasut dengan tanah menentang tarikan pasukan lawan. Pasukan boleh meningkatkan daya geseran dengan:
◦ Memakai kasut dengan tapak yang lebih mencengkam (pekali geseran lebih tinggi).
◦ Menambah jumlah jisim pasukan (contohnya, memilih ahli yang lebih berat), kerana daya geseran maksimum adalah berkadar dengan daya tindak balas normal, yang berkaitan dengan berat.
2. Mengoptimumkan Sudut Badan: Dengan merendahkan pusat graviti dan mencondongkan badan ke belakang pada sudut yang lebih besar, ahli pasukan boleh menggunakan berat badan mereka dengan lebih berkesan. Meleraikan berat (W) mereka kepada komponen-komponen akan menghasilkan komponen daya yang selari dengan tanah yang membantu menentang tarikan lawan, sebagai tambahan kepada daya yang dihasilkan oleh otot kaki dan belakang. Ini meningkatkan daya keseluruhan yang dikenakan ke tanah.
