Nota Sains Tingkatan 4 Bab 11: Daya Dan Gerakan
RINGKASAN
Ringkasan Komprehensif (Nota Sains Tingkatan 4 Bab 11: Daya Dan Gerakan)
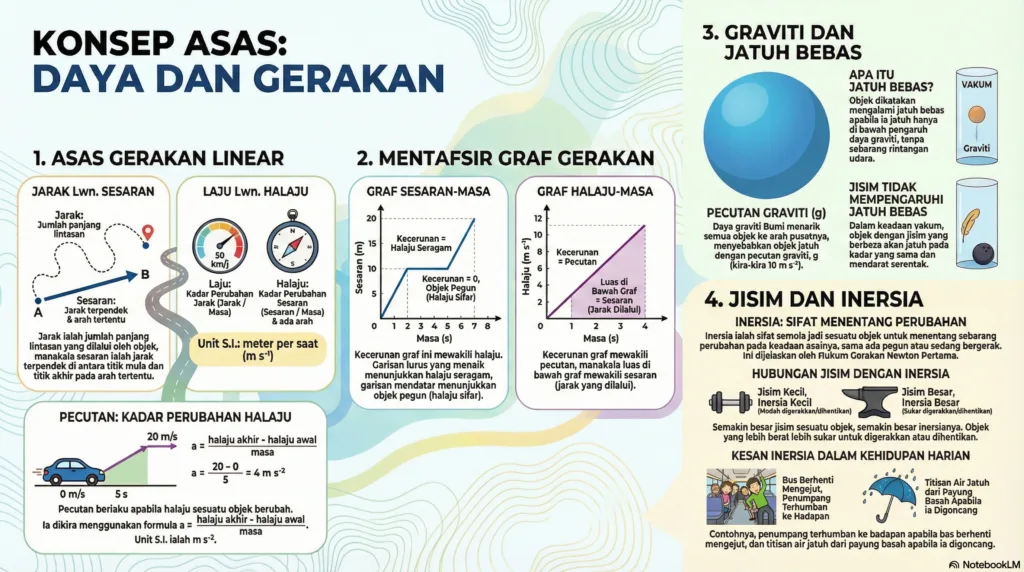
Bab ini meneroka konsep asas daya dan gerakan, memfokuskan kepada empat bidang utama: Gerakan Linear, Graf Gerakan Linear, Pecutan Graviti dan Jatuh Bebas, serta Jisim dan Inersia.
1. Gerakan Linear
Gerakan linear ialah gerakan suatu objek dalam lintasan yang lurus. Konsep-konsep asas dalam gerakan linear ialah:
• Jarak: Jumlah panjang lintasan yang dilalui oleh suatu objek. Ia adalah kuantiti skalar.
• Sesaran: Jarak lintasan terpendek yang menyambungkan dua lokasi dalam satu arah tertentu. Ia adalah kuantiti vektor.
• Laju: Kadar perubahan jarak. Unit S.I. ialah meter per saat (m s⁻¹). Formula: Laju = Jarak / Masa
• Laju Purata: Kadar perubahan jumlah jarak yang dilalui. Formula: Laju Purata = Jumlah Jarak / Jumlah Masa
• Halaju: Kadar perubahan sesaran. Ia adalah kuantiti vektor yang menyatakan kelajuan dan arah gerakan. Unit S.I. ialah meter per saat (m s⁻¹). Formula: Halaju = Sesaran / Masa
• Pecutan: Kadar perubahan halaju. Objek mengalami pecutan apabila halajunya bertambah. Unit S.I. ialah meter per saat per saat (m s⁻²). Formula: Pecutan (a) = (Halaju Akhir (v) - Halaju Awal (u)) / Masa (t)
• Nyahpecutan: Berlaku apabila halaju objek berkurang.
2. Graf Gerakan Linear
Graf digunakan untuk menyampaikan maklumat tentang gerakan dengan lebih jelas. Terdapat dua jenis graf utama:
• Graf Sesaran-Masa: Menunjukkan bagaimana sesaran suatu objek berubah dengan masa.
◦ Kecerunan graf mewakili halaju objek.
◦ Garis lurus dengan kecerunan positif: Halaju seragam.
◦ Garis lurus dengan kecerunan sifar (mendatar): Objek dalam keadaan rehat (halaju sifar).
◦ Garis lurus dengan kecerunan negatif: Halaju seragam pada arah bertentangan.
• Graf Halaju-Masa: Menunjukkan bagaimana halaju suatu objek berubah dengan masa.
◦ Kecerunan graf mewakili pecutan objek.
◦ Luas di bawah graf mewakili sesaran objek.
◦ Kecerunan positif: Pecutan seragam.
◦ Kecerunan sifar (garis mendatar): Pecutan sifar (halaju malar/seragam).
◦ Kecerunan negatif: Nyahpecutan seragam.
3. Pecutan Graviti dan Jatuh Bebas
• Daya Graviti Bumi: Daya yang menarik objek ke arah pusat Bumi.
• Pecutan Graviti (g): Pecutan yang dialami oleh objek disebabkan oleh daya graviti. Di permukaan Bumi, nilai pecutan graviti, g, ialah kira-kira 10 m s⁻².
• Jatuh Bebas: Gerakan suatu jasad yang dipengaruhi oleh daya graviti sahaja. Ini hanya berlaku dalam keadaan vakum (tiada rintangan udara). Dalam vakum, objek dengan jisim yang berbeza akan jatuh dengan pecutan yang sama dan mendarat pada masa yang sama jika dilepaskan dari ketinggian yang sama.
4. Jisim dan Inersia
• Jisim: Kuantiti jirim dalam sesuatu objek. Unit S.I. ialah kilogram (kg). Jisim ialah ukuran kuantitatif bagi inersia.
• Inersia: Sifat semula jadi sesuatu objek yang cenderung menentang sebarang perubahan keadaan asalnya, sama ada dalam keadaan pegun atau sedang bergerak.
• Hubungan Jisim dan Inersia: Semakin besar jisim sesuatu objek, semakin besar inersia objek tersebut. Objek yang lebih berat lebih sukar untuk digerakkan dari keadaan pegun atau dihentikan dari keadaan bergerak.
• Hukum Gerakan Newton Pertama: Menyatakan bahawa sesuatu objek akan kekal dalam keadaan asalnya, iaitu sama ada pegun atau bergerak dengan laju malar (dalam garis lurus) jika tiada daya luar yang bertindak terhadapnya. Ini selaras dengan konsep inersia.
• Kesan Inersia: Boleh memberi kesan positif (cth: mengeringkan payung dengan memutarkannya) dan negatif (cth: kecederaan akibat pergerakan badan ke hadapan apabila kenderaan berhenti mengejut).
GLOSARI
| Istilah | Definisi |
| Jarak | Jumlah panjang lintasan yang dilalui oleh suatu objek. |
| Sesaran | Jarak lintasan terpendek yang menyambungkan dua lokasi dalam satu arah tertentu. |
| Laju | Kadar perubahan jarak. Formula: Jarak / Masa. |
| Halaju | Kadar perubahan sesaran. Ia mempunyai magnitud (laju) dan arah. Formula: Sesaran / Masa. |
| Laju Purata | Kadar perubahan jumlah jarak yang dilalui. Formula: Jumlah Jarak / Jumlah Masa. |
| Pecutan | Kadar perubahan halaju. Berlaku apabila halaju objek bertambah. Formula: a = (v-u)/t. |
| Nyahpecutan | Pecutan negatif; berlaku apabila halaju objek berkurang. |
| Graf Sesaran-Masa | Graf yang memplotkan sesaran objek melawan masa. Kecerunannya mewakili halaju. |
| Graf Halaju-Masa | Graf yang memplotkan halaju objek melawan masa. Kecerunannya mewakili pecutan dan luas di bawah graf mewakili sesaran. |
| Pecutan Graviti (g) | Pecutan yang dialami oleh objek akibat tindakan daya graviti sahaja. Nilainya di permukaan Bumi ialah kira-kira 10 m s⁻². |
| Jatuh Bebas | Keadaan gerakan suatu objek yang hanya dipengaruhi oleh daya graviti, tanpa kehadiran rintangan udara atau daya luar lain. |
| Jisim | Kuantiti jirim yang terkandung di dalam suatu objek. Unit S.I. ialah kilogram (kg). |
| Inersia | Sifat semula jadi suatu objek yang cenderung menentang sebarang perubahan keadaan asalnya sama ada dalam keadaan pegun atau sedang bergerak. |
| Hukum Gerakan Newton Pertama | Menyatakan bahawa objek akan kekal pegun atau bergerak dengan halaju malar jika tiada daya luar yang bertindak ke atasnya. |
| Pita Detik | Alat yang digunakan di dalam makmal untuk mengkaji gerakan objek dengan membuat siri titik pada pita kertas pada sela masa yang tetap (cth: 50 Hz atau 0.02 s setiap detik). |
CONTOH SOALAN KBAT
Soalan KBAT (Kemahiran Berfikir Aras Tinggi)
1. Soalan: Ali memandu dari bandar A ke bandar B yang terletak 120 km ke timur, dan mengambil masa 2 jam. Dia kemudian berpatah balik dan memandu ke bandar C yang terletak 30 km ke barat dari bandar B, mengambil masa 30 minit. Bandingkan laju purata dan halaju purata bagi keseluruhan perjalanan Ali dari A ke C.
Jawapan:
• Jumlah Jarak: 120 km (A ke B) + 30 km (B ke C) = 150 km.
• Jumlah Masa: 2 jam + 0.5 jam = 2.5 jam.
• Laju Purata: Jumlah Jarak / Jumlah Masa = 150 km / 2.5 j = 60 km/j.
• Sesaran: Dari A, kedudukan akhir C ialah 120 km – 30 km = 90 km ke timur.
• Halaju Purata: Sesaran / Jumlah Masa = 90 km / 2.5 j = 36 km/j ke arah timur.
• Kesimpulan: Laju purata (60 km/j) adalah lebih besar daripada magnitud halaju purata (36 km/j) kerana jarak yang dilalui lebih besar daripada sesaran akhir dari titik permulaan.
2. Soalan: Semasa misi bantuan banjir, sebuah helikopter perlu menggugurkan bekalan makanan ke kawasan terpencil. Bekalan itu perlu mendarat dengan perlahan untuk mengelakkan kerosakan. Dengan menggunakan konsep jatuh bebas dan rintangan udara, cadangkan satu reka bentuk payung terjun yang sesuai untuk bekalan tersebut. Jelaskan jawapan anda.
Jawapan:
• Cadangan: Bekalan makanan perlu dipasang pada payung terjun yang mempunyai saiz kanopi yang besar dan diperbuat daripada bahan yang ringan tetapi kuat.
• Penjelasan: Objek yang jatuh di udara dipengaruhi oleh graviti dan rintangan udara. Untuk memperlahankan kejatuhan (mengurangkan halaju akhir), rintangan udara perlu dimaksimumkan. Kanopi payung terjun yang besar akan memerangkap lebih banyak udara, mewujudkan daya seretan (rintangan udara) yang lebih tinggi untuk menentang daya graviti. Ini akan menyebabkan bekalan tersebut mengalami nyahpecutan dan mencapai halaju akhir yang lebih rendah, lalu mendarat dengan lebih perlahan dan selamat.
3. Soalan: Jelaskan mengapa lebih sukar untuk menolak sebuah troli yang penuh dengan barangan berbanding troli yang kosong, menggunakan konsep jisim dan inersia.
Jawapan:
• Troli yang penuh dengan barangan mempunyai jisim yang lebih besar berbanding troli yang kosong.
• Inersia ialah sifat objek untuk menentang perubahan dalam keadaan gerakannya. Hubungan antara jisim dan inersia adalah berkadar terus; semakin besar jisim, semakin besar inersia.
• Oleh itu, troli yang penuh (jisim besar) mempunyai inersia yang lebih besar. Ini bermakna ia mempunyai kecenderungan yang lebih tinggi untuk kekal dalam keadaan pegun. Daya yang lebih besar diperlukan untuk mengatasi inersianya yang besar dan memulakan pergerakan.
4. Soalan: Sebuah kereta mainan bergerak di atas landasan. Graf halaju-masanya menunjukkan garis lurus yang condong ke atas dari (0s, 0 m/s) ke (5s, 10 m/s), diikuti oleh garis mendatar sehingga 10s, dan kemudian garis lurus yang condong ke bawah ke (15s, 0 m/s). Tafsirkan gerakan kereta mainan itu dan hitung jumlah sesarannya.
Jawapan:
• Tafsiran Gerakan:
◦ 0s – 5s: Kereta mainan bergerak dengan pecutan seragam. Pecutan = (10-0)/5 = 2 m s⁻².
◦ 5s – 10s: Kereta mainan bergerak dengan halaju malar/seragam 10 m s⁻¹ (pecutan sifar).
◦ 10s – 15s: Kereta mainan bergerak dengan nyahpecutan seragam sehingga berhenti. Nyahpecutan = (0-10)/5 = -2 m s⁻².
• Pengiraan Jumlah Sesaran: Jumlah sesaran ialah luas di bawah graf halaju-masa, yang berbentuk trapezium.
◦ Luas = ½ × (jumlah sisi selari) × tinggi
◦ Luas = ½ × ((10-5) + 15) × 10
◦ Luas = ½ × (5 + 15) × 10
◦ Luas = ½ × 20 × 10 = 100 m.
◦ Jumlah sesaran kereta mainan ialah 100 m.
5. Soalan: Galileo Galilei dikatakan telah menjalankan eksperimen dengan melepaskan dua peluru meriam yang berbeza jisim dari Menara Condong Pisa. Dia mendapati kedua-duanya mendarat pada masa yang hampir sama. Bagaimanakah eksperimen ini menyokong konsep jatuh bebas? Mengapakah masa pendaratan mereka “hampir sama” dan tidak betul-betul sama?
Jawapan:
• Sokongan Konsep Jatuh Bebas: Eksperimen ini menyokong idea bahawa pecutan graviti tidak bergantung pada jisim objek. Dalam keadaan ideal (jatuh bebas), semua objek, tanpa mengira jisimnya, akan jatuh dengan pecutan yang sama (g ≈ 10 m s⁻²) dan mengambil masa yang sama untuk sampai ke tanah jika dilepaskan dari ketinggian yang sama.
• Penjelasan “Hampir Sama”: Masa pendaratan hanya “hampir sama” kerana eksperimen itu dijalankan di udara, bukan dalam vakum. Ini bermakna kedua-dua objek dipengaruhi oleh rintangan udara. Walaupun peluru meriam padat dan rintangan udara mempunyai kesan yang kecil berbanding daya graviti, ia masih wujud dan boleh menyebabkan perbezaan masa yang sangat kecil antara kedua-dua objek. Untuk pemerhatian yang sempurna, eksperimen perlu dijalankan dalam vakum.
